Conceived by Edsger W. Dijsktra in 1956 and published three years later, Dijkstra’s algorithm is a one of the most known algorithms for finding the shortest paths between nodes in a graph. This algorithm is applied in a lot of domains. For example, once you have represented road networks in a graph, it becomes easy to calculate shortest paths inside this graph by applying Dijkstra’s algorithm.

In Pseudocode, Dijkstra’s algorithm can be translated like that :

dijkstra_pseudo_code

In this tutorial, you’re going to learn how to implement Disjkstra’s Algorithm in Java. In a first time, we need to create objects to represent a graph before to apply Dijkstra’s Algorithm.

1. Represent Edges

In a graph, Edges are used to link two Nodes. So, an Edge is linked to two nodes and have a length that is an integer here. It’s useful to represent a distance for example in road networks.

?
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
package com.ssaurel.dijsktra;
 
public class Edge {
 
  private int fromNodeIndex;
  private int toNodeIndex;
  private int length;
 
  public Edge(int fromNodeIndex, int toNodeIndex, int length) {
    this.fromNodeIndex = fromNodeIndex;
    this.toNodeIndex = toNodeIndex;
    this.length = length;
  }
 
  public int getFromNodeIndex() {
    return fromNodeIndex;
  }
 
  public int getToNodeIndex() {
    return toNodeIndex;
  }
 
  public int getLength() {
    return length;
  }
 
  // determines the neighbouring node of a supplied node, based on the two nodes connected by this edge
  public int getNeighbourIndex(int nodeIndex) {
    if (this.fromNodeIndex == nodeIndex) {
      return this.toNodeIndex;
    } else {
      return this.fromNodeIndex;
   }
  }
 
}

 

2. Represent Nodes

Now, it’s time to represent Nodes. A Node must have a list of Edge that are linked to it. Besides, it must have a field to define if the Node has been visited or no. It will be useful when we will apply Dijkstra’s Algorithm to calculate shortest paths in the graph. Last, we need to define a distanceFromSource field that will represent the result for that Node of the algorithm.

?
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
package com.ssaurel.dijsktra;
 
import java.util.ArrayList;
 
public class Node {
 
  private int distanceFromSource = Integer.MAX_VALUE;
  private boolean visited;
  private ArrayList<Edge> edges = new ArrayList<Edge>(); // now we must create edges
 
  public int getDistanceFromSource() {
    return distanceFromSource;
  }
 
  public void setDistanceFromSource(int distanceFromSource) {
    this.distanceFromSource = distanceFromSource;
  }
 
  public boolean isVisited() {
    return visited;
  }
 
  public void setVisited(boolean visited) {
    this.visited = visited;
  }
 
  public ArrayList<Edge> getEdges() {
    return edges;
  }
 
  public void setEdges(ArrayList<Edge> edges) {
    this.edges = edges;
  }
 
}

 

3. Represent a Graph

Now that we have Edges and Nodes, we can represent a Graph that must contain Edges and Nodes. In the constructor, we take an array of Edges and we build the Graph by creating corresponding Nodes. The Dijkstra’s Algorithm is implemented in the calculateShortestDistances() method. It’s really the application of the Pseudocode algorithm displayed previously. Our Graph class is like that :

?
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
package com.ssaurel.dijsktra;
 
import java.util.ArrayList;
 
// now we must create graph object and implement dijkstra algorithm
public class Graph {
 
  private Node[] nodes;
  private int noOfNodes;
  private Edge[] edges;
  private int noOfEdges;
 
  public Graph(Edge[] edges) {
    this.edges = edges;
 
    // create all nodes ready to be updated with the edges
    this.noOfNodes = calculateNoOfNodes(edges);
    this.nodes = new Node[this.noOfNodes];
 
    for (int n = 0; n < this.noOfNodes; n++) {
      this.nodes[n] = new Node();
    }
 
    // add all the edges to the nodes, each edge added to two nodes (to and from)
    this.noOfEdges = edges.length;
 
    for (int edgeToAdd = 0; edgeToAdd < this.noOfEdges; edgeToAdd++) {
      this.nodes[edges[edgeToAdd].getFromNodeIndex()].getEdges().add(edges[edgeToAdd]);
      this.nodes[edges[edgeToAdd].getToNodeIndex()].getEdges().add(edges[edgeToAdd]);
    }
 
  }
 
  private int calculateNoOfNodes(Edge[] edges) {
    int noOfNodes = 0;
 
    for (Edge e : edges) {
      if (e.getToNodeIndex() > noOfNodes)
        noOfNodes = e.getToNodeIndex();
      if (e.getFromNodeIndex() > noOfNodes)
        noOfNodes = e.getFromNodeIndex();
    }
 
    noOfNodes++;
 
    return noOfNodes;
  }
 
  // next video to implement the Dijkstra algorithm !!!
  public void calculateShortestDistances() {
    // node 0 as source
    this.nodes[0].setDistanceFromSource(0);
    int nextNode = 0;
 
    // visit every node
    for (int i = 0; i < this.nodes.length; i++) {
      // loop around the edges of current node
      ArrayList<Edge> currentNodeEdges = this.nodes[nextNode].getEdges();
 
      for (int joinedEdge = 0; joinedEdge < currentNodeEdges.size(); joinedEdge++) {
        int neighbourIndex = currentNodeEdges.get(joinedEdge).getNeighbourIndex(nextNode);
 
        // only if not visited
        if (!this.nodes[neighbourIndex].isVisited()) {
          int tentative = this.nodes[nextNode].getDistanceFromSource() + currentNodeEdges.get(joinedEdge).getLength();
 
          if (tentative < nodes[neighbourIndex].getDistanceFromSource()) {
            nodes[neighbourIndex].setDistanceFromSource(tentative);
          }
        }
      }
 
      // all neighbours checked so node visited
      nodes[nextNode].setVisited(true);
 
      // next node must be with shortest distance
      nextNode = getNodeShortestDistanced();
 
   }
  }
 
  // now we're going to implement this method in next part !
  private int getNodeShortestDistanced() {
    int storedNodeIndex = 0;
    int storedDist = Integer.MAX_VALUE;
 
    for (int i = 0; i < this.nodes.length; i++) {
      int currentDist = this.nodes[i].getDistanceFromSource();
 
      if (!this.nodes[i].isVisited() && currentDist < storedDist) {
        storedDist = currentDist;
        storedNodeIndex = i;
      }
    }
 
    return storedNodeIndex;
  }
 
  // display result
  public void printResult() {
    String output = "Number of nodes = " + this.noOfNodes;
    output += "\nNumber of edges = " + this.noOfEdges;
 
    for (int i = 0; i < this.nodes.length; i++) {
      output += ("\nThe shortest distance from node 0 to node " + i + " is " + nodes[i].getDistanceFromSource());
    }
 
    System.out.println(output);
  }
 
  public Node[] getNodes() {
    return nodes;
  }
 
  public int getNoOfNodes() {
    return noOfNodes;
  }
 
  public Edge[] getEdges() {
    return edges;
  }
 
  public int getNoOfEdges() {
    return noOfEdges;
  }
 
}

In the printResult() method, we have just to iterate on the Nodes’ array and display the distanceFromSource property value.

 

4. Assemble the puzzle in a Main class

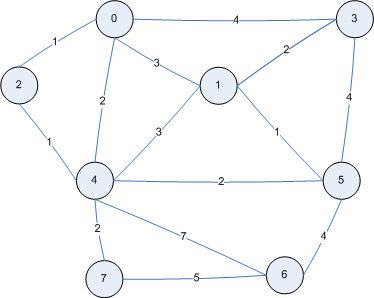
Now, it’s time to test our implementation of the Dijkstra’s Algorithm. So, we consider the following graph :

graph

 

We define that graph in our Main class and then we have just to call the calculateShortestDistances() method. Last, we need to print the result of the algorithm.

?
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
package com.ssaurel.dijsktra;
 
public class Main {
 
  public static void main(String[] args) {
    Edge[] edges = {
      new Edge(0, 2, 1), new Edge(0, 3, 4), new Edge(0, 4, 2),
      new Edge(0, 1, 3), new Edge(1, 3, 2), new Edge(1, 4, 3),
      new Edge(1, 5, 1), new Edge(2, 4, 1), new Edge(3, 5, 4),
      new Edge(4, 5, 2), new Edge(4, 6, 7), new Edge(4, 7, 2),
      new Edge(5, 6, 4), new Edge(6, 7, 5)
    };
 
    Graph g = new Graph(edges);
    g.calculateShortestDistances();
    g.printResult(); // let's try it !
  }
 
}

 

Result is detailed in the following figure.

Capture d’écran 2016-05-18 à 22.39.53

Like you can see, our implementation works well !

 

5. Bonus

As a Bonus, you can enjoy the following tutorial in video :